Three Tips to Keep Students Engaged during Math Class: Part 1


There is more to student engagement in math class than just having good classroom management. Sure, all of your students may be behaving well, but are they engaged, participating, and confidently interacting during your lesson?
I believe student engagement begins with how intentional you are in building a strong classroom community amongst the mathematicians that are in your class
Although these tips may seem simple, they can be the difference between students who have shut down or given up during your math block and students who are engaged and eager to take risks while learning.
I’ll be sharing simple tips that are sure to keep your students engaged during any math lesson.
Tip #1: Empathy
“It is wonderful to be loved, it is profound to be understood.” – Ellen DeGeneres
Do you think empathy plays a role in math class? I would say empathy is one of THE most important things to show our students, especially during math instruction.
Specifically in math, we tend to wander around the class, only looking for the students who are “getting the answer right,” instead of observing students to understand what they understand.
When we call on students we are listening to hear if the answer they have provided is what we are hoping to hear. We aren’t listening for what they understand. When it isn’t what we were hoping for, we quickly move to another student who can help us get to where we want to be.
When we do this, we bypass the moment and forget about empathy. Although it may not be the answer we were looking to get from the student, there is merit in giving an answer and therefore, it requires acknowledgment.
Acknowledgement is not just saying: “Oh good try, Suzy. Anyone else?”
It can look like saying:
“Tell me more…”
“Wow, let me see if I understand what you mean…”

I was once co-teaching a math class of fourth graders. The lesson for that day was to introduce division. Although they had been exposed to division in third grade, these particular students were continuing to build their understanding of it.
The lesson began with a launching question the students were to solve to connect to their previous learning around division concepts.
We asked the students to solve the problem however they liked, but to also include an equation(s) to match their work.
The problem was:
There were 12 cookies that I needed to share with my three children. How many cookies did each child get?
I didn’t anticipate this being a difficult question, but I did remind students that division meant equal shares, repeated subtraction, etc., before we dove into the math standard of remainders.
Hot tip: In order to guide my instruction more authentically, I purposely didn’t say something like, “What do you remember about division?” It felt much more of an authentic launch and formative assessment to just present a problem and to see what students would do.
The students were divided into partners to solve this problem. One set of partners used their manipulatives to solve and then wrote the following equations on their boards.
(manipulatives were in groups of 4 originally, moving the board shifted them– focus on the equation here)

My first thought was to correct their thinking and say something like, “No, when we use that division symbol, we write like this…”
Instead, I remembered about leading my reactions with empathy. I put myself in their shoes and thought:
- What were they thinking?
- Why did they do that?
- What do they know and understand? (your students always know and understand SOMETHING)
So, I said:
“OHHH, what an interesting idea! I love how you wrote that. May I use your board to help us learn more about this problem?”
The students agreed to show their board and I brought it to the document camera along with a handful of other boards to share out and help us build a common understanding of division.
I had several students write the division equation ‘correctly,’ but just showing what is ‘right’ doesn’t help students understand WHY it is right and it doesn’t build the collective efficacy of the group to only share ‘correct’ thinking. In fact, doing so results in more shutting down.
Students will start thinking:
My teacher only cares about the right answers.
If I don’t know for sure I can get it right, why should I try?
To avoid this, I continue coming from a place of empathy and share these students’ boards and ask the class, “What do you think these students were thinking? Why do you think they wrote it like this?”
At first, the students look at the work confused. They want to correct it and argue that it’s wrong (possibly a trait learned from a previous teacher?).
When I don’t get an answer, I insert another question to keep the thinking alive and the students engaged. This also prevents students from shaming the work that is displayed.
“Think of what these mathematicians knew about how we write equations and how they used that to help them with this. I TOTALLY understand why they did this and I think it’s genius.”
Read that again: I totally understand why they did this.
Imagine how empowering it must feel for your student when you equip them with the confidence of knowing that it’s okay to try, even if they are not sure if the answer is “right” every time.
Most of the class is a bit perplexed, but they humor me. The two students who did this equation are smiling from ear to ear.
Their ideas were validated.
They are understood for what they were thinking, not for the correctness of their equation format.
“I get it!” One student exclaims. “That’s how we write addition!” I then help make sense of this connection for the rest of the class.
I continue discussing,“Can’t we write addition like this (vertically with the addition sign)? What about multiplication? What about subtraction?” We write sample equations on the board.
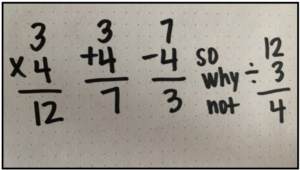
I end our class discussion with:
“Wow. What great mathematicians. Mathematicians make use of structure. These guys were thinking, if that’s how we write for the other operations,why not division?”
This prompted a fabulous conversation about how we actually write the equations (correctly). As a class, we conclude that these students’ ideas weren’t correct, but boy was it clever.
Your goal as a teacher in every math lesson is to understand what your students understand and let them know that their thinking and problem solving skills are worth paying attention to. This keeps them engaged, confident, and most importantly- trying!
If you enjoyed these ideas, you may like my FREE resources available to ALL math teachers!
Access your free math resources here:
https://www.empowerlearngrow.com/login?redirecturl=resources

 Shannon Kiebler
Shannon Kiebler 